An Ontology of Segregation: Difference between revisions
No edit summary |
No edit summary |
||
| Line 12: | Line 12: | ||
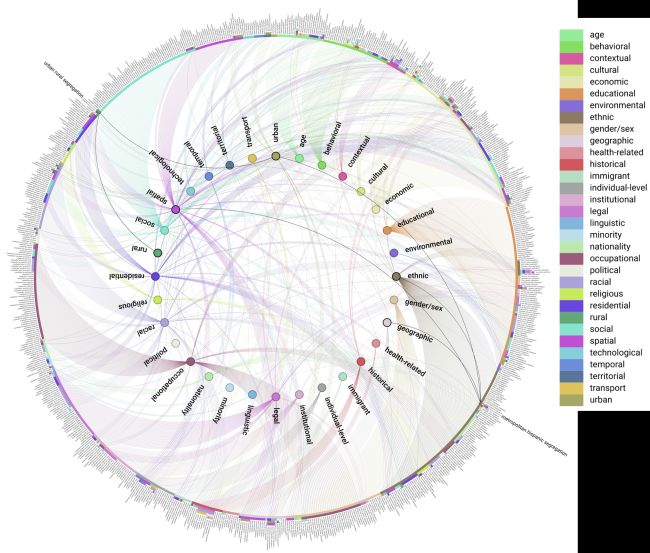
After clustering, we constructed the taxonomy. Each SF could belong to one or more types, with only one SF being assigned a maximum of 8 types. Each ST is associated with a cluster as a node in its local network of directly related SFs. As SFs may belong to different clusters, they form a network of relationships between SFs and their types, leading to an integrated, semi-hierarchical taxonomy of 32 distinct segregation types. This method allows us to identify key groupings and the overall relational structure of SFs. We produced a network graph (Fig. 17) using color and size to distinguish between SFs and types, making it easier to interpret how different forms of segregation relate to specific taxonomical categories. This visualization highlights the differences in complexity between various SFs, offering the means to access their categorization and relationships. | After clustering, we constructed the taxonomy. Each SF could belong to one or more types, with only one SF being assigned a maximum of 8 types. Each ST is associated with a cluster as a node in its local network of directly related SFs. As SFs may belong to different clusters, they form a network of relationships between SFs and their types, leading to an integrated, semi-hierarchical taxonomy of 32 distinct segregation types. This method allows us to identify key groupings and the overall relational structure of SFs. We produced a network graph (Fig. 17) using color and size to distinguish between SFs and types, making it easier to interpret how different forms of segregation relate to specific taxonomical categories. This visualization highlights the differences in complexity between various SFs, offering the means to access their categorization and relationships. | ||
[[File:The segregation taxonomy.jpg|center|650x650px | [[File:The segregation taxonomy.jpg|center|650x650px|'''Fig. 17''' – Network representation of the segregation taxonomy: the inner ring contains the 32 types, the outer ring contains the 804 identified SFs. Colors represent the types. The lines connect each type with all the SFs that they are associated with. The colored dots in the SF ring show the types associated with each SF. Two randomly selected SFs and their corresponding types are highlighted. Navigate the complete [https://cityscience.group/segregation-ontology/ taxonomy network].]] | ||
Revision as of 18:21, 9 October 2024
We have identified and mapped hundreds of forms of segregation across a diverse scientific literature encompassing 169 disciplinary fields, revealing the extraordinary connectivity between these forms. Given the complexity of this mosaic, how can we make it more comprehensible and valuable to the multidisciplinary community of researchers studying segregation and its many dimensions? A taxonomy offers a means to bring semantic organization to this heterogeneous field. Derived from the Greek words taxis (arrangement or order) and nomos (science), a taxonomy is a systematic classification framework (Hedden, 2016) that organizes phenomena into categories based on shared characteristics, features, components, and the relationships among them. There are several approaches to developing a taxonomy (Hedden, 2016; Kundisch et al., 2022; Kwasnik, 1999; Nickerson et al., 2013). In this paper, we propose an inductive, bottom-up approach to taxonomy creation. Additionally, we define the nature of the relationships and typological positions that various forms of segregation occupy within this taxonomic space based on the following definitions:
i. Segregation form refers to a specific act, practice, or process of separating or restricting interaction between individuals or social groups based on distinguishing characteristics, such as race, income, religion, or other social attributes. These forms are manifested through observable social, spatial, material, or economic patterns. Segregation forms are context-dependent, reflecting how segregation forces manifest within a particular environment, time, or population, shaping and being shaped by the surrounding societal, cultural, and economic conditions.
ii. Segregation type is a broader conceptual category that encompasses multiple related forms of segregation. Types represent a generalization of shared underlying structures, processes or properties that may manifest through distinct but related forms. For example, residential segregation might be considered a type that encompasses various forms, such as income-based or ethnic-based residential segregation. The defining feature of a type is its ability to group specific forms based on common socio-economic, spatial, or institutional mechanisms, allowing for general patterns of segregation to be identified across various contexts.
Segregation forms can intersect and belong to multiple types. For instance, 'metropolitan Hispanic segregation' encompasses ethnic, geographic, urban and spatial segregation forms (Fig. 17). The taxonomic method should, therefore, avoid a strictly hierarchical structure, making relationships exclusively vertical, as found in dendrogram-like taxonomies in biology, opting instead for a richer relational approach. The method should also identify typological relationships between segregation forms and types from the bottom up, meaning that such relationships emerge from information produced or latent in the literature.
We employed a natural language processing (NLP) approach to group and rank SFs based on their semantic similarity using hierarchical clustering. First, the SFs were converted into high-dimensional numerical representations (embeddings) using a pre-trained sentence transformer model, specifically the all-mpnet-base-v2 from Sentence Transformers. These embeddings capture the semantic relationships between the SFs. We evaluated multiple models, including SciBERT (allenai/scibert_scivocab_uncased) (Beltagy et al., 2019)), BERT (bert-large-uncased) (Devlin et al., 2018), MPNet (sentence-transformers/ all-mpnet-base-v2) (Song et al., 2020), and T5 (t5-large) (Raffel et al., 2020), using combinations of distance metrics (cosine, euclidean) and clustering methods (ward, average, complete). The sentence-transformers/all-mpnet-base-v2 model is trained on large-scale datasets such as MultiNLI (for natural language inference), MS MARCO (for question answering and information retrieval), and TriviaQA (for question-answer pairs) (sentence-transformers/all-mpnet-base-v2 [Model]. Hugging Face, 2021)(Hugging Face, 2021), enabling it to generate high-quality sentence embeddings by learning relationships between sentences across diverse tasks like semantic similarity, inference, and factual understanding. After testing different configurations, we found that the MPNet model with cosine distance and complete linkage produced the most semantically meaningful clusters. This combination allowed for more distinct separations between groups, particularly in capturing the nuanced, multi-dimensional relationships between SFs. When computing semantic similarity for rare or specialised terms like "elderly residential segregation," general language models may struggle due to insufficient contextual understanding and poor representation of these terms in their training data. This can lead to inaccurate similarity scores, as the model may overemphasise more frequent components of the phrase (e.g. 'residential' over 'elderly') and fail to capture the nuanced meaning of the rare term. However, we found this only rarely to be the case in our application.
The complexity of semantic clustering for SFs lies in the fact that some SFs can theoretically belong to multiple clusters. For instance, ethnic residential segregation could cluster with both economic residential segregation (as they both address residential segregation) and ethnic school segregation (as they both involve ethnicity). Meanwhile, economic residential segregation and ethnic school segregation do not share a semantic commonality. This overlap in thematic relationships made it difficult to rely solely on traditional clustering metrics such as silhouette score or Davies–Bouldin index, which fail to account for such intersections. Manual evaluation, therefore, was necessary to assess the coherence and interpretability of the clusters. Multiple authors with expert knowledge qualitatively associated SFs with relevant labels, following predefined criteria developed in the coding phase of this research (see the codebook in SI) to reduce subjectivity and ensure consistent assessment. Clusters were assessed based on their ability to group SFs that shared similar meanings or contexts and were assigned with labels. We identified 32 labels able to sufficiently represent such clusters of common features as segregation types (STs).
After clustering, we constructed the taxonomy. Each SF could belong to one or more types, with only one SF being assigned a maximum of 8 types. Each ST is associated with a cluster as a node in its local network of directly related SFs. As SFs may belong to different clusters, they form a network of relationships between SFs and their types, leading to an integrated, semi-hierarchical taxonomy of 32 distinct segregation types. This method allows us to identify key groupings and the overall relational structure of SFs. We produced a network graph (Fig. 17) using color and size to distinguish between SFs and types, making it easier to interpret how different forms of segregation relate to specific taxonomical categories. This visualization highlights the differences in complexity between various SFs, offering the means to access their categorization and relationships.